Teoría de selección de carteras (I): conceptos teóricos

Por Daniel García.

En 1990, se otorgó el Premio Nobel de Economía a Harry Markowitz, Merton Miller y William Sharpe por sus trabajos en el campo de las finanzas. Hoy vamos a hablar de la contribución del primero, la llamada "teoría de selección de carteras", "teoría moderna de carteras" o "análisis media-varianza".

Hasta 1952, se consideraba que el riesgo de una cartera venía dado por el comportamiento individual de sus componentes. Por ejemplo, si un inversor estaba pensando en adquirir acciones de una aerolínea, solo se preocupaba por estudiar su rentabilidad esperada (en estadística, la esperanza es la media). Markowitz se dio cuenta de que esta manera de abordar la selección de valores no era óptima. Lo correcto sería tratar a la cartera como un todo. Si en un escenario económico cualquiera el comportamiento de una editorial tradicional de libros es opuesto al desempeño de una empresa dedicada a la fabricación de ebooks, ¿acaso esto no es importante para el inversor? Esto es lo que trató Markowitz en su famoso artículo.

Desde luego, no sería lo mismo que estas dos empresas tuviesen un coeficiente de correlación de 1, que de -1. Este número simplemente indica cómo se mueven a lo largo del tiempo con respecto a la otra. Si el coeficiente es 1, las dos se moverán exactamente igual, al unísono. Si es de -1, cuando una suba un 10% la otra bajará otro tanto, y viceversa. Si es de 0, no existiría ninguna relación entre las cotizaciones de las compañías.

¿Qué es lo que le interesa a un inversor? Maximizar la rentabilidad esperada y minimizar el riesgo. Esto parece algo coherente: nadie está dispuesto a soportar mayores vaivenes en sus ahorros para finalmente obtener un resultado menor. Este, precedido por los supuestos de que la rentabilidad se mide por la esperanza y el riesgo por la volatilidad (mediante medidas de dispersión como la varianza), es el tercer axioma del modelo. Son más o menos coherentes, aunque no están exentos de críticas. Pero esa es otra historia.

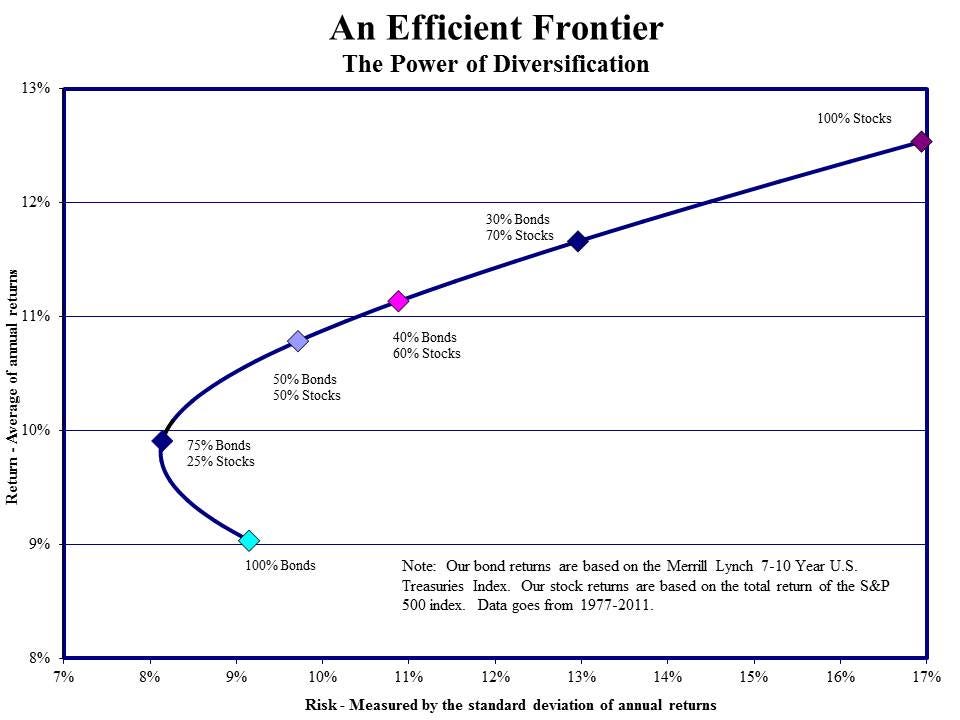
¿Cómo se hace algo así? Si echamos un vistazo al artículo o a cualquier página web que explique el modelo, veremos que las fórmulas y expresiones matemáticas pueden perdernos. Así que voy a intentar explicarlo de manera simple. Siguiendo con el ejemplo de la editorial y la empresa de ebooks: el primer paso consiste en dibujar un gráfico que relacione la volatilidad de la cartera (eje horizontal) y su rentabilidad esperada (eje vertical). ¿Cuáles serían las diferentes carteras? Una en la que la editorial pese el 100% y la empresa de ebooks pese el 0%, otra cuyas proporciones sean 90%-10%, otra con 80%-20%... hasta 0%-100%. Nos quedaría algo así, llamado "frontera eficiente":

Nota: para que fuese una frontera eficiente habría que suprimir el tramo inferior, desde 100% Bonds hasta 75% Bonds-25% Stocks. A ese nivel de riesgo del 9% y rentabilidad esperada del 9%, existe otra combinación superior.

En la imagen se habla de acciones y bonos, pero todo es análogo. Un activo A y un activo B, repartidos con diferentes pesos en carteras sucesivas. Como estos dos activos no solo no se comportan de igual manera, sino que su éxito es opuesto (es de esperar que si los consumidores se lanzan a demandar ebooks, esta empresa prospere y la editorial decaiga, y viceversa), el coeficiente de correlación sea negativo.

Esto permitiría obtener un cierto reparto en el que el riesgo sea mínimo (MVP, minimum variance portfolio o cartera de mínima varianza). De hecho, si el coeficiente fuese perfectamente -1, la varianza sería... ¡cero! En el gráfico, obtendríamos un punto sobre el eje de ordenadas, lo que es equivalente a pensar en una rentabilidad libre de riesgo fruto de la combinación óptima de dos activos inversamente correlacionados. Por supuesto, en la vida real esto no existe. Pero es una buena aproximación para entender que lo importante no son los activos individualmente, sino como grupo.

"Todo esto está muy bien, pero antes has dicho que el inversor prefiere más riesgo solo si retorna una mayor rentabilidad. Y en la frontera eficiente la relación entre rentabilidad y riesgo es positiva. ¿Cómo sabríamos cuál elegir?" Muy bien visto. En la frontera eficiente, no hay una cartera perfecta para todos los individuos. Su elección dependerá de sus curvas de indiferencia. Esto es, cuánto riesgo adicional están dispuestos a soportar a cambio de un poco más de rentabilidad esperada.

Cada persona tiene infinitas curvas de indiferencia en su cabeza, al menos en teoría. Cada una representa un conjunto de carteras que proporcionan el mismo bienestar al individuo y, en este caso, cuanto más hacia arriba se ubique, mayor bienestar reportará. Por ejemplo, ¿por qué en el gráfico anterior no se toma la cartera en la que la curva C1 corta a la frontera eficiente si es la que más rentabilidad da? Pues porque la curva C3 es superior: se aleja más del origen (está por encima de C1) y además es tangencial a la frontera eficiente. Este es el punto óptimo para este inversor en cuestión.

Es posible que esta última idea de las curvas de indiferencia se les escape a algunas personas. No pasa nada. Lo importante del modelo es que se debe mirar el desempeño total de la cartera, y no el de sus activos uno por uno. Esa es la conclusión del modelo y es lo que merece la pena entender.