Bienvenidos a una nueva serie de artículos. En esta ocasión veremos aspectos que se deberían enseñar en los colegios desde bien temprano (se debería, pero no se hace). La realidad es que las matemáticas financieras siguen siendo algo oscuro para la mayoría de la población.
Quienes tengan al menos una base en este tema puede que vean esto demasiado básico, pero no es así. Para muestra, un botón: más de la mitad de los españoles no sabe reconocer el interés compuesto. Así que este parece un buen asunto para inaugurar la serie: explicar la diferencia entre el interés simple y el compuesto.
La fórmula del interés simple es sencilla. Involucra un capital inicial y un tipo de interés. Nada más. Por ejemplo, si contratamos un depósito a plazo fijo en el banco por el que recibimos un 2% al cabo de un año y dedicamos 10.000€ a este depósito, los elementos son:
- Capital inicial: 10.000€ depositados
- Tasa de interés: 2% (0,02 en términos unitarios)
No hace falta nada más para calcular el capital final, que ascenderá a 10.200€.
Pero claro, esto puede ser engañoso, porque la fórmula no dice nada acerca del plazo en el que se obtiene el dinero. Si hubiese otro depósito con las mismas características pero a 6 meses, también devolvería 10.200€.
Por eso es importante dejar claro cuál es el horizonte temporal considerado para el pago de intereses. Pero con un simple arreglo es posible comparar el pago de interés simple en estos dos instrumentos financieros, uno a un año y otro a 6 meses.
Si tenemos acceso al depósito de 6 meses, podríamos invertir el mismo capital dos veces en un año, por así decirlo. Imaginemos dos líneas temporales, una para el depósito anual y otra para el semestral. En el primer caso, no hay pasos intermedios. La inversión termina al cabo de un año y se pagan unos intereses por importe de 200€. Pero en el segundo, el acuerdo termina a la mitad de la línea, y ahí se reciben 200€ más el capital original. El inversor puede renovar el depósito (a veces esto se hace automáticamente) y volver a depositar los 10.000€, marchándose con 200€ en el bolsillo en ese momento y consiguiendo 200€ más al cabo de 6 meses.
La fórmula para saber los intereses totales es muy sencilla. Basta con multiplicar el capital inicial (Ci) por el tipo de interés (i) por el número de repeticiones en el periodo (n). En este caso, 10.000 × 0,02 × 2. Si hablásemos de 5 años, bastaría sustituir n = 2 por n = 10 (dos veces cada año en cinco años).
Hasta ahí tenemos la explicación del interés simple. La del interés compuesto, si hemos entendido esta, no supone problemas. Solo hay que considerar que esos intereses pagados no llegan a nuestro bolsillo, sino que pasan a formar parte del capital inicial. De esta manera, el principal sobre el que se calculan los intereses es cada vez mayor, por lo que devuelve más ganancias cuanto más tiempo lo dejemos funcionar.
La fórmula es muy parecida a la anterior, solo que el elemento de la tasa de interés se eleva al número de periodos que dure la inversión. Volviendo al ejemplo del depósito semestral, el eje quedaría así:
A los 6 meses no se "recibiría" nada, sino que esos 200€ devengados engrosarían el capital inicial, permitiendo que al cabo del año el pago total fuese de 10.404€. No parece una gran diferencia (esto depende del tipo de interés y el tiempo que se considere), pero a largo plazo se obtendría algo así:
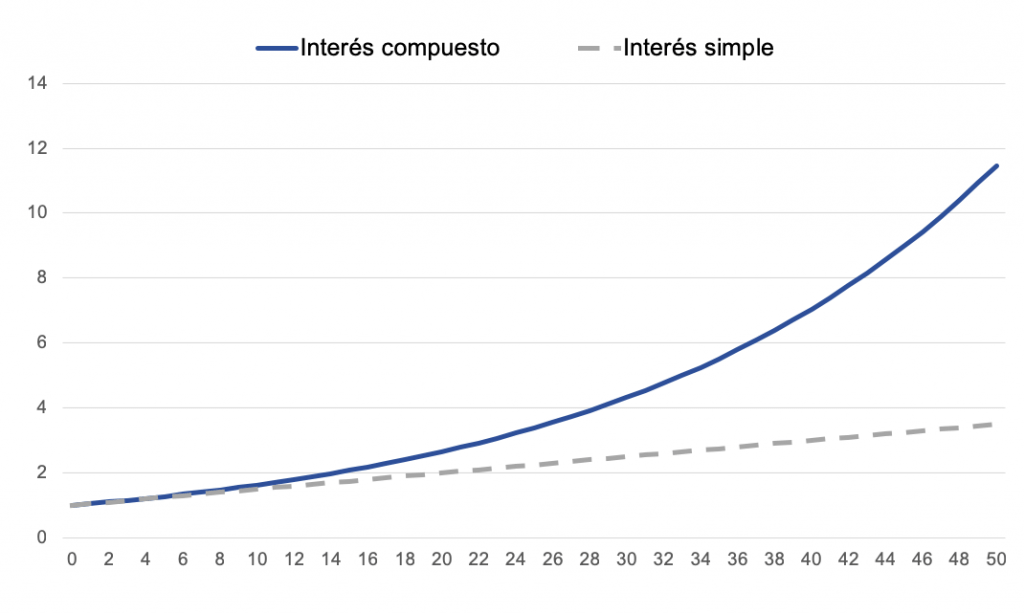
Ese es el potencial del interés compuesto: una evolución exponencial frente al rendimiento lineal del interés fijo. Algo que en el futuro lejano cambia mucho las cosas. Y, aun así, únicamente menos de la mitad de españoles lo conocen.




Comentarios
Publicar un comentario
Deja aquí tu comentario.